A confidence interval is an estimate in statistics drawn from a sample population to evaluate the overall population value. This type of measurement is important when aiming to assess the level of certainty or uncertainty in statistics.
Inhaltsverzeichnis
- 1 Confidence Interval – In a Nutshell
- 2 Definition: Confidence interval
- 3 When do you use a confidence interval?
- 4 Calculating a confidence interval
- 5 Confidence interval in normal distribution
- 6 Confidence interval for proportions
- 7 Confidence interval in non-normal distribution
- 8 Reporting the confidence interval
- 9 Confidence interval – Common misinterpration
- 10 FAQs
- 11 Sources
Confidence Interval – In a Nutshell
- Confidence interval is used to make an estimate in statistics.
- When making estimates based on a sample population, you must develop a range of values where your estimate would fall if you redid your experiment.1
- These values are calculated based on the alpha value.
Definition: Confidence interval
Confidence in statistics refers to probability.
The confidence interval refers to the average of your estimate in statistics, including the negative or positive variations. The desired confidence is usually one minus the alpha value applied in the statistical test: (1 − a).2
When do you use a confidence interval?
You use confidence intervals for diverse statistical estimates like proportions, population means, and variations between population means and proportions. The confidence interval helps to communicate the difference surrounding the point estimate.
Example: Confidence Interval
A survey was conducted on 100 Asians and 100 Americans about their phone-using habits. This survey showed that both groups spent an average of 35 hours on their phone weekly.
Even so, the number of Asians surveyed showed a higher variation in the number of hours they spent on the phone, while Americans all spent similar amounts of time on their phones.
While both groups had the same point estimate, the Asian estimates’ variation created a wider confidence interval than the American estimate.
Calculating a confidence interval
There are certain aspects a student needs to consider before calculating the confidence interval. These include:
- The point of estimate
- Critical values used in the statistic test
- The standard deviation of the sample
- The sample size
Point estimate
The point estimate refers to the statistical estimate the student makes.
Example:
In the scenario above, the point estimate is the average amount of time spent using a phone is 35 hours
Critical value
The critical value guides the students on the number of standard deviations they need to achieve their desired confidence level for the confidence interval.
To find the critical values, you need to follow these three steps:
- Choose the alpha value:
The alpha value refers to the probability verge for statistical importance. The most used alpha value is p=0.05, but you can use 0.1, 0.01, or 0.001.
- Decide between one-tailed and two-tailed:
In the case of the two-tailed interval, you should divide the alpha value by two to get the alpha values of the higher and lower tails.
- Find the corresponding critical value:
For normal distribution or when the sample size is larger than thirty, you can use the z-distribution to find the critical values.
Here are some of the common values used for z statistics:
| Confidence Level: | 90%, 95%, 99% |
| Alpha for one-tailed CI: | 0.1, 0.05, 0.01 |
| Alpha for two-tailed CI: | 0.05, 0.025, 0.005 |
| Z statistic: | 1.64, 1.96, 2.57 |
A student should use a t distribution in the case of small datasets with normal distribution.
Example:
In the above survey, there are more than 30 observations, and the data set follows a bell curve, so you should apply the z distribution.
The confidence interval = 95%
Alpha value = 0.025
The corresponding critical value = 1.9
Therefore, the confidence interval is the average of ±1.96 from the average.
Standard deviation
The student should find the data’s sample variance and then perform a square root to get the standard deviation.3
- Find sample variance:
You can find the sample variance by adding the squared differences from the average, also referred to as mean-squared-error (MSE):
= Sample variance = The value of the one observation = The mean value of all observation =The number of observation
To get the MSE, deduct the sample mean from each value in the data set, square it, and divide the result by the sample size: -1 (n-1).
Add all these values to find the total sample variance .
- Square root sample variance:
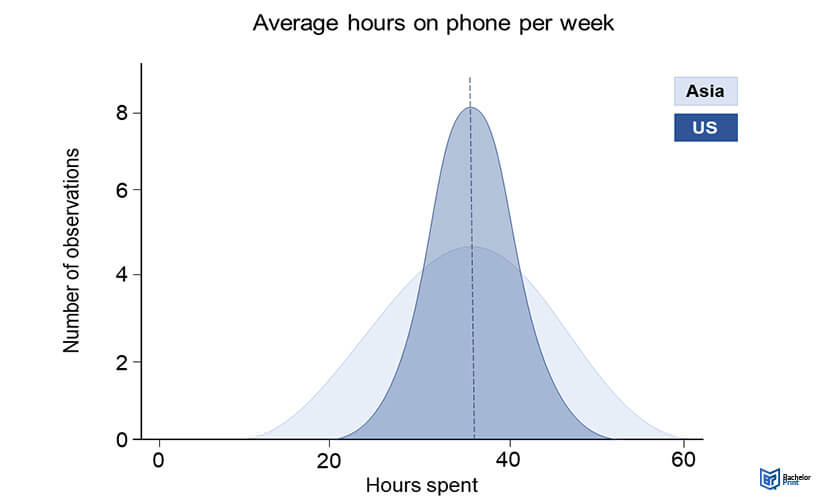
In the example above, the variance in the Asian estimate is 100, while the variance in the US estimate is 25. The square roots are 10 and 5, respectively.
Sample size
The sample size refers to the total observations in a data set. In the above survey, the sample size is 100 Americans and 100 Asians.
Confidence interval in normal distribution
The confidence interval in this case is:
= The population mean = The critical value of the z distribution = The population standard deviation = The square root of the sample size
In the case of a t distribution, use the same formula but replace Z* with t*.
Example:
In the above survey, one can plug in values in this formula based on a 95% confidence level.
| US |
|
| Asia |
|
The confidence intervals for the US participants are 34.02 and 35.98, while the Asian confidence intervals are 33.04 and 36.96.
Confidence interval for proportions
You should use the same formula for proportions, but the SD, in this case, equates to the same proportion multiplied by one subtracting the proportion.
= Proportion of the sample = Critical value of z distribution = Sample size
Confidence interval in non-normal distribution
There are two methods that you can use to calculate the confidence interval for data with non-normal distribution:
- Find a distribution that matches the shape of your data:
Apply this distribution to get the confidence interval.
- Data transformation to make it fit a normal distribution:
Perform a reverse transformation on data, then calculate the maximum and minimum bounds of the confidence interval.
Reporting the confidence interval
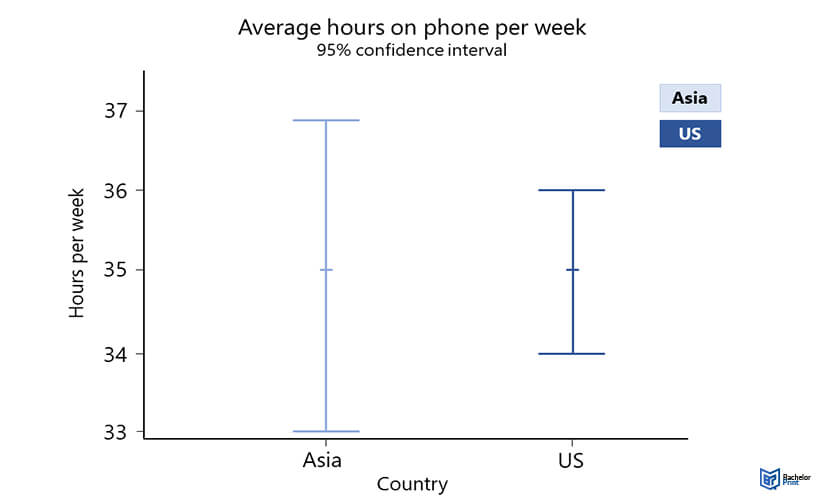
When reporting the confidence interval in papers, include the higher and lower bounds of the confidence level.
Example:
The Asian data set has more variation with a 95% CI= 33.04, 36.96, and the American set is 95% CI = 34.02, 35.98.
They are used in graphs when demonstrating variations between groups, variations around estimates, and creating a linear regression.
Example:
In the above scenario, you can plot using the point estimate of the average hours participants use phones in Asia and the US, along with a 95% confidence level
Confidence interval – Common misinterpration
A common misinterpretation is that the real value of one’s estimate is between the higher and lower range of the confidence interval.
This is false, as the CI is calculated using a sample rather than an entire population.
FAQs
To determine how good an estimate is. The higher the CI, the more caution you should take.
The number of observations in a statistical sample.
The square root of sample variance.
Sources
1 National Library of Medicine. “Confidence Intervals.” Accessed January 2, 2023. https://www.nlm.nih.gov/nichsr/stats_tutorial/section2/mod2_confidence.html.
2 Zhang, Jing, Bruce W. Hanik and Beth H. Chaney. “Confidence Intervals: Evaluating and Facilitating Their Use in Health Education Research.” The Health Educator 40, no. 1 (Spring, 2008): 29-36. https://files.eric.ed.gov/fulltext/EJ863507.pdf.
3 Sullivan, Lisa. “Confidence Intervals.” Boston University School of Public Health. Accessed January 2, 2023. https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/bs704_confidence_intervals_print.html.